9
Linear Function Approximation
A probability distribution representation is used to describe return functions
in terms of a collection of numbers that can be stored in a computer’s mem-
ory. With it, we can devise algorithms that operate on return distributions in a
computationally efficient manner, including distributional dynamic program-
ming algorithms and incremental algorithms such as CTD and QTD. Function
approximation arises when our representation of the value or return function
uses parameters that are shared across states. This allows reinforcement learning
methods to be applied to domains where it is impractical or even impossible to
keep in memory a table with a separate entry for each state, as we have done
in preceding chapters. In addition, it makes it possible to make predictions
about states that have not been encountered – in effect, to generalize a learned
estimate to new states.
As a concrete example, consider the problem of determining an approxima-
tion to the optimal value function for the game of Go. In Go, players take turns
placing white and black stones on a 19
×
19 grid. At any time, each location of
the board is either occupied by a white or black stone, or unoccupied; conse-
quently, there are astronomically many possible board states.
67
Any practical
algorithm for this problem must therefore use a succinct representation of its
value or return function.
Function approximation is also used to apply reinforcement learning algo-
rithms to problems with continuous state variables. The classic Mountain Car
domain, in which the agent must drive an underpowered car up a steep hill, is
one such problem. Here, the state consists of the car’s position and velocity
(both bounded on some interval); learning to control the car requires being able
67.
A naive estimate is 3
19×19
. The real figure is somewhat lower due to symmetries and the
impossibility of certain states.
Draft version. 261
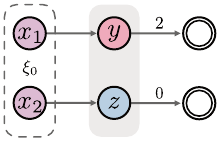
262 Chapter 9
Figure 9.1
A Markov decision process in which aliasing due to function approximation may result
in the wrong value function estimates even at the unaliased states x
1
and x
2
.
to map two-dimensional points to a desired action, usually by predicting the
return obtained following this action.
68
While there are similarities between the use of probability distribution rep-
resentations (parameterizing the output of a return function) and function
approximation (parameterizing its input), the latter requires a different algorith-
mic treatment. When function approximation is required, it is usually because
it is infeasible to exhaustively enumerate the state space and apply dynamic
programming methods. One solution is to rely on samples (of the state space,
transitions, trajectories, etc.), but this results in additional complexities in the
algorithm’s design. Combining incremental algorithms with function approxi-
mation may result in instability or even divergence; in the distributional setting,
the analysis of these algorithms is complicated by two levels of approximation
(one for probability distributions and one across states). With proper care, how-
ever, function approximation provides an effective way of dealing with large
reinforcement learning problems.
9.1 Function Approximation and Aliasing
By necessity, when parameters are shared across states, a single parameter usu-
ally affects the predictions (value or distribution) at multiple states. In this case,
we say that the states are aliased. State aliasing has surprising consequences in
the context of reinforcement learning, including the unwanted propagation of
errors and potential instability in the learning process.
Example 9.1.
Consider the Markov decision process in Figure 9.1, with four
nonterminal states
x
1
, x
2
, y
, and
z
, a single action, a deterministic reward
function, an initial state distribution
ξ
0
, and no discounting. Consider an
68.
Domains such as Mountain Car – which have a single initial state and a deterministic transition
function – can be solved without function approximation: for example, by means of a search
algorithm. However, function approximation allows us to learn a control policy that can in theory
be applied to any given state and has a low run-time cost.
Draft version.
Linear Function Approximation 263
approximation based on three parameters w
x
1
, w
x
2
, and w
yz
, such that
ˆ
V(x
1
) = w
x
1
ˆ
V(x
2
) = w
x
2
ˆ
V(y) =
ˆ
V(z) = w
yz
.
Because the rewards from
y
and
z
are different, no choice of
w
yz
can yield
ˆ
V = V
π
. As such, any particular choice of w
yz
trades off approximation error at
y
and
z
. When a reinforcement learning algorithm is combined with function
approximation, this trade-off is made (implicitly or explicitly) based on the
algorithm’s characteristics and the parameters of the learning process. For
example, the best approximation obtained by the incremental Monte Carlo
algorithm (Section 3.2) correctly learns the value of x
1
and x
2
:
ˆ
V(x
1
) = 2 ,
ˆ
V(x
2
) = 0 ,
but learns a parameter
w
yz
that depends on the frequency at which states
y
and
z
are visited. This is because
w
yz
is updated toward 2 whenever the estimate
ˆ
V
(
y
) is updated and toward 0 whenever
ˆ
V
(
z
) is updated. In our example, the
frequency at which this occurs is directly implied by the initial state distribution
ξ
0
, and we have
w
yz
= 2 ×P
π
(X
1
= y) + 0 ×P
π
(X
1
= z)
= 2ξ
0
(x
1
) . (9.1)
When the approximation is learned using a bootstrapping procedure, aliasing
can also result in incorrect estimates at states that are not themselves aliased.
The solution found by temporal-difference learning,
w
yz
, is as per Equation 9.1,
but the algorithm also learns the incorrect value at x
1
and x
2
:
ˆ
V(x
1
) =
ˆ
V(x
2
) = 0 + γ ×
ˆ
V(z)
= 2ξ
0
(x
1
) .
Thus, errors due to function approximation can compound in unexpected ways;
we will study this phenomenon in greater detail in Section 9.3. 4
In a linear value function approximation, the value estimate at a state
x
is
given by a weighted combination of features of
x
. This is in opposition to a
tabular representation, where value estimates are stored in a table with one
entry per state.
69
As we will see, linear approximation is simple to implement
and relatively easy to analyze.
Definition 9.2.
Let
n ∈N
+
. A state representation is a mapping
φ
:
X→R
n
.
A linear value function approximation
V
w
∈R
X
is parameterized by a weight
69.
Technically, a tabular representation can also be expressed using the trivial collection of indicator
features. In practice, the two are used in distinct problem settings.
Draft version.
264 Chapter 9
vector w ∈R
n
and maps states to their expected return estimates according to
V
w
(x) = φ(x)
>
w .
A feature
φ
i
(
x
)
∈R
,
i
= 1
, . . . , n
is an individual element of
φ
(
x
). We call the
vectors φ
i
∈R
X
basis functions. 4
As its name implies, a linear value function approximation is linear in the
weight vector w. That is, for any w
1
, w
2
∈R
n
, α, β ∈R, we have
V
αw
1
+βw
2
= αV
w
1
+ βV
w
2
.
In addition, the gradient of V
w
(x) with respect to w is given by
∇
w
V
w
(x) = φ(x) .
As we will see, these properties affect the learning dynamics of algorithms that
use linear value function approximation.
We extend linear value function approximation to state-action values in the
usual way. For a state representation φ : X×A→R
n
, we define
Q
w
(x, a) = φ(x, a)
>
w .
A practical alternative is to use a distinct set of weights for each action and a
common representation
φ
(
x
) across actions. In this case, we use a collection of
weight vectors (w
a
: a ∈A), with w
a
∈R
n
, and write
Q
w
(x, a) = φ(x)
>
w
a
.
Remark 9.1 discusses the relationship between these two methods.
9.2 Optimal Linear Value Function Approximations
In this chapter, we will assume that there is a finite (but very large) number
of states. In this case, the state representation
φ
:
X→R
n
can expressed as a
feature matrix Φ
∈R
X×n
whose rows are the vectors
φ
(
x
),
x ∈X
. This yields the
approximation
V
w
= Φw .
The state representation determines a space of value function approximations
that are constructed from linear combinations of features. Expressed in terms of
the feature matrix, this space is
F
φ
= {Φw : w ∈R
n
}.
We first consider the problem of finding the best linear approximation to a value
function
V
π
. Because
F
φ
is a
n
-dimensional linear subspace of the space of
value functions
R
X
, there are necessarily some value functions that cannot be
represented with a given state representation (unless
n
=
N
X
). We measure the
Draft version.

Linear Function Approximation 265
discrepancy between a value function
V
π
and an approximation
V
w
= Φ
w
in
ξ-weighted L
2
norm, for ξ ∈P(X):
kV
π
−V
w
k
ξ,2
=
X
x∈X
ξ(x)
V
π
(x) −V
w
(x)
2
1
/2
.
The weighting
ξ
reflects the relative importance given to different states. For
example, we may weigh states according to the frequency at which they are
visited, or we may put greater importance on initial states. Provided that
ξ
(
x
)
>
0
for all x ∈X, the norm k·k
ξ,2
induces the ξ-weighted L
2
metric on R
X
:
70
d
ξ,2
(V, V
0
) = kV −V
0
k
ξ,2
.
The best linear approximation under this metric is the solution to the
minimization problem
min
w∈R
n
kV
π
−V
w
k
ξ,2
. (9.2)
One advantage of measuring approximation error in a weighted
L
2
norm, rather
than the
L
∞
norm used in the analyses of previous chapters, is that a solution
w
∗
to Equation 9.2 can be easily determined by solving a least-squares system.
Proposition 9.3.
Suppose that the columns of the feature matrix Φ are
linearly independent and
ξ
(
x
)
>
0 for all
x ∈X
. Then, Equation 9.2 has a
unique solution w
∗
given by
w
∗
= (Φ
>
ΞΦ)
−1
Φ
>
ΞV
π
, (9.3)
where Ξ ∈R
X×X
is a diagonal matrix with entries (ξ(x) : x ∈X). 4
Proof. By a standard calculus argument, any optimum w must satisfy
∇
w
X
x∈X
ξ(x)
V
π
(x) −φ(x)
>
w
2
= 0
=⇒
X
x∈X
ξ(x)
V
π
(x) −φ(x)
>
w
φ(x) = 0 .
Written in matrix form, this is
Φ
>
Ξ(Φw −V
π
) = 0
=⇒ Φ
>
ΞΦw = Φ
>
ΞV
π
.
70.
Technically,
k·k
ξ,2
is only a proper norm if
ξ
is strictly positive for all
x
; otherwise, it is
a semi-norm. Under the same condition,
d
ξ,2
is proper metric; otherwise, it is a pseudo-metric.
Assuming that ξ(x) > 0 for all x addresses uniqueness issues and simplifies the analysis.
Draft version.

266 Chapter 9
Because Φ has rank
n
, then so does Φ
>
ΞΦ: for any
u ∈R
n
with
u ,
0, we have
Φu = v , 0 and so
u
>
Φ
>
ΞΦu = v
>
Ξv
=
X
x∈X
ξ(x)v(x)
2
> 0 ,
as
ξ
(
x
)
>
0 and
v
(
x
)
2
≥
0 for all
x ∈X
, and
P
x∈X
v
(
x
)
2
>
0. Hence, Φ
>
ΞΦ is
invertible and the only solution w
∗
to the above satisfies Equation 9.3.
9.3 A Projected Bellman Operator for Linear Value Function
Approximation
Dynamic programming finds an approximation to the value function
V
π
by
successively computing the iterates
V
k+1
= T
π
V
k
.
As we saw in preceding chapters, dynamic programming makes it easy to derive
incremental algorithms for learning the value from samples and also allows us to
find an approximation to the optimal value function
Q
∗
. Often, it is the de facto
approach for finding an approximation of the return-distribution function. It is
also particularly useful when using function approximation, where it enables
algorithms that learn by extrapolating to unseen states.
When dynamic programming is combined with function approximation, we
obtain a range of methods called approximate dynamic programming. In the case
of linear value function approximation, the iterates (
V
k
)
k≥0
are given by linear
combinations of features, which allows us to apply dynamic programming to
problems with larger state spaces than can be described in memory. In general,
however, the space of approximations
F
φ
is not closed under the Bellman
operator, in the sense that
V ∈F
φ
6=⇒ T
π
V ∈F
φ
.
Similar to the notion of a distributional projection introduced in Chapter 5, we
address the issue by projecting, for
V ∈R
X
, the value function
T
π
V
back onto
F
φ
. Let us define the projection operator Π
φ,ξ
: R
X
→R
X
as
(Π
φ,ξ
V)(x) = φ(x)
>
w
∗
such that w
∗
∈arg min
w∈R
n
kV −V
w
k
ξ,2
.
This operator returns the approximation
V
w
∗
= Φ
w
∗
that is closest to
V ∈R
X
in the
ξ
-weighted
L
2
norm. As established by Proposition 9.3, when
ξ
is fully
supported on
X
and the basis functions (
φ
i
)
n
i=1
are linearly independent, then this
Draft version.
Linear Function Approximation 267
projection is unique.
71
By repeatedly applying the projected Bellman operator
Π
φ,ξ
T
π
from an initial condition V
0
∈F
φ
, we obtain the iterates
V
k+1
= Π
φ,ξ
T
π
V
k
. (9.4)
Unlike the approach taken in Chapter 5, however, it is usually impractical
to implement Equation 9.4 as is, as there are too many states to enumerate.
A simple solution is to rely on a sampling procedure that approximates the
operator itself. For example, one may sample a batch of
K
states and find the
best linear fit to
T
π
V
k
at these states. In the next section, we will study the
related approach of using an incremental algorithm to learn the linear value
function approximation from sample transitions. Understanding the behavior
of the exact projected operator Π
φ,ξ
T
π
informs us about the behavior of these
approximations, as it describes in some sense the ideal behavior that one expects
from both of these approaches.
Also different from the setting of Chapter 5 is the presence of aliasing across
states. As a consequence of this aliasing, we have limited freedom in the choice
of projection if we wish to guarantee the convergence of the iterates of Equation
9.4. To obtain such a guarantee, in general, we need to impose a condition on
the distribution
ξ
that defines the projection Π
φ,ξ
. We will demonstrate that
the projected Bellman operator is a contraction mapping with modulus
γ
with
respect to the
ξ
-weighted
L
2
norm, for a specific choice of
ξ
. Historically, this
approach predates the analysis of distributional dynamic programming and is in
fact a key inspiration for our analysis of distributional reinforcement learning
algorithms as approximating projected Bellman operators (see bibliographical
remarks).
To begin, let us introduce the convention that the Lipschitz constant of an
operator with respect to a norm (such as
L
∞
) follows Definition 5.20, applied to
the metric associated with the norm. In the case of
L
∞
, this metric defines the
distance between u, u
0
∈R
X
by
ku −u
0
k
∞
.
Now recall that the Bellman operator
T
π
is a contraction mapping in
L
∞
norm,
with modulus
γ
. One reason this holds is because the transition matrix
P
π
satisfies
kP
π
uk
∞
≤kuk
∞
, for all u ∈R
X
;
71.
If only the first of those two conditions hold, then there may be multiple optimal weight vectors.
However, they all result in the same value function, and the projection remains unique.
Draft version.
268 Chapter 9
we made use of this fact in the proof of Proposition 4.4. This is equivalent to
requiring that the Lipschitz constant of P
π
satisfy
kP
π
k
∞
≤1 .
Unfortunately, the Lipschitz constant of Π
φ,ξ
in the
L
∞
norm may be greater
than 1, precluding a direct analysis in that norm (see Exercise 9.5). We instead
prove that the Lipschitz constant of
P
π
in the
ξ
-weighted
L
2
norm satisfies the
same condition when
ξ
is taken to be a steady-state distribution under policy
π
.
Definition 9.4.
Consider a Markov decision process and let
π
be a policy
defining the probability distribution
P
π
over the random transition (
X, A, R, X
0
).
We say that ξ ∈P(X) is a steady-state distribution for π if for all x
0
∈X,
ξ(x
0
) =
X
x∈X
ξ(x)P
π
(X
0
= x
0
| X = x) . 4
Assumption 9.5.
There is a unique steady-state distribution
ξ
π
, and it satisfies
ξ
π
(x) > 0 for all x ∈X. 4
Qualitatively, Assumption 9.5 ensures that approximation error at any state
is reflected in the norm
k·k
ξ
π
,2
; contrast with the setting in which
ξ
π
is nonzero
only at a handful of states. Uniqueness is not strictly necessary but simplifies the
exposition. There are a number of practical scenarios in which the assumption
does not hold, most importantly when there is a terminal state. We discuss how
to address such a situation in Remark 9.2.
Lemma 9.6.
Let
π
:
X→P
(
A
) be a policy and let
ξ
π
be a steady-state distri-
bution for this policy. The transition matrix is a nonexpansion with respect to
the ξ
π
-weighted L
2
metric. That is,
kP
π
k
ξ
π
,2
= 1 . 4
Proof.
A simple algebraic argument shows that if
U ∈R
X
is such that
U
(
x
) = 1
for all x, then
P
π
U = U .
This shows that kP
π
k
ξ
π
,2
≥1. Now for an arbitrary U ∈R
X
, write
kP
π
Uk
2
ξ
π
,2
=
X
x∈X
ξ
π
(x)
(P
π
U)(x)
2
=
X
x∈X
ξ
π
(x)
X
x
0
∈X
P
π
(x
0
| x)U(x
0
)
2
(a)
≤
X
x∈X
ξ
π
(x)
X
x
0
∈X
P
π
(x
0
| x)
U(x
0
)
2
Draft version.

Linear Function Approximation 269
=
X
x
0
∈X
U(x
0
)
2
X
x∈X
ξ
π
(x)P
π
(x
0
| x)
(b)
=
X
x
0
∈X
ξ
π
(x
0
)
U(x
0
)
2
= kUk
2
ξ
π
,2
,
where (a) follows by Jensen’s inequality and (b) by Definition 9.4. Since
kP
π
k
ξ
π
,2
= sup
U∈R
X
kP
π
Uk
ξ
π
,2
kUk
ξ
π
,2
≤1 ,
this concludes the proof.
Lemma 9.7.
For any
ξ ∈P
(
X
) with
ξ
(
x
)
>
0, the projection operator Π
φ,ξ
is a
nonexpansion in the ξ-weighted L
2
metric, in the sense that
kΠ
φ,ξ
k
ξ,2
= 1 . 4
The proof constitutes Exercise 9.4.
Theorem 9.8.
Let
π
be a policy and suppose that Assumption 9.5 holds;
let
ξ
π
be the corresponding steady-state distribution. The projected Bellman
operator Π
φ,ξ
π
T
π
is a contraction with respect to the
ξ
π
-weighted
L
2
norm
with modulus γ, in the sense that for any V, V
0
∈R
X
,
kΠ
φ,ξ
π
T
π
V −Π
φ,ξ
π
T
π
V
0
k
ξ
π
,2
≤γkV −V
0
k
ξ
π
,2
.
As a consequence, this operator has a unique fixed point
ˆ
V
π
= Π
φ,ξ
π
T
π
ˆ
V
π
, (9.5)
which satisfies
k
ˆ
V
π
−V
π
k
ξ
π
,2
≤
1
p
1 −γ
2
kΠ
φ,ξ
π
V
π
−V
π
k
ξ
π
,2
. (9.6)
In addition, for an initial value function V
0
∈R
X
, the sequence of iterates
V
k+1
= Π
φ,ξ
π
T
π
V
k
(9.7)
converges to this fixed point. 4
Proof.
The contraction result and consequent convergence of the iterates in
Equation 9.7 to a unique fixed point follow from Lemmas 9.6 and 9.7, which,
combined with Lemma 5.21, allow us to deduce that
kΠ
φ,ξ
π
T
π
k
ξ
π
,2
≤γ .
Draft version.

270 Chapter 9
Because Assumption 9.5 guarantees that
k·k
ξ
π
,2
induces a proper metric, we
may then apply Banach’s fixed-point theorem. For the error bound of Equation
9.6, we use Pythagoras’s theorem to write
k
ˆ
V
π
−V
π
k
2
ξ
π
,2
= k
ˆ
V
π
−Π
φ,ξ
π
V
π
k
2
ξ
π
,2
+ kΠ
φ,ξ
π
V
π
−V
π
k
2
ξ
π
,2
= kΠ
φ,ξ
π
T
π
ˆ
V
π
−Π
φ,ξ
π
T
π
V
π
k
2
ξ
π
,2
+ kΠ
φ,ξ
π
V
π
−V
π
k
2
ξ
π
,2
≤γ
2
k
ˆ
V
π
−V
π
k
2
ξ
π
,2
+ kΠ
φ,ξ
π
V
π
−V
π
k
2
ξ
π
,2
,
since
k
Π
φ,ξ
π
T
π
k
ξ
π
,2
≤γ
. The result follows by rearranging terms and taking the
square root of both sides.
Theorem 9.8 implies that the iterates (
V
k
)
k≥0
are guaranteed to converge
when the projection is performed in
ξ
π
-weighted
L
2
norm. Of course, this does
not imply that a projection in a different norm may not result in a convergent
algorithm (see Exercise 9.8), but divergence is a practical concern (we return to
this point in the next section). A sound alternative to imposing a condition on
the distribution
ξ
is to instead impose a condition on the feature matrix Φ; this
is explored in Exercise 9.10.
When the feature matrix Φ forms a basis of
R
X
(i.e., it has rank
N
X
), it is
always possible to find a weight vector w
∗
for which
Φw
∗
= T
π
V ,
for any given V ∈R
X
. As a consequence, for any ξ ∈P (X) we have
Π
φ,ξ
T
π
= T
π
,
and Theorem 9.8 reduces to the analysis of the (unprojected) Bellman operator
given in Section 4.2. On the other hand, when
n < N
X
, the fixed point of Equation
9.5 is in general different from the minimum-error solution Π
φ,ξ
π
V
π
and is
called the temporal-difference learning fixed point. Similar to the diffusion
effect studied in Section 5.8, successive applications of the projected Bellman
operator result in compounding approximation errors. The nature of this fixed
point is by now well studied in the literature (see bibliographical remarks).
9.4 Semi-Gradient Temporal-Difference Learning
We now consider the design of a sample-based, incremental algorithm for
learning the linear approximation of a value function
V
π
. In the context of
domains with large state spaces, algorithms that learn from samples have an
advantage over dynamic programming approaches: whereas the latter require
some form of enumeration and hence have a computational cost that depends
on the size of
X
, the computational cost of the former instead depends on the
Draft version.
Linear Function Approximation 271
size of the function approximation (in the linear case, on the number of features
n).
To begin, let us consider learning a linear value function approximation using
an incremental Monte Carlo algorithm. We are presented with a sequence of
state-return pairs (
x
k
, g
k
)
k≥0
, with the assumption that the source states
x
k
are
realizations of independent draws from the distribution
ξ
and that each
g
k
is a
corresponding independent realization of the random return
G
π
(
x
k
). As before,
we are interested in the optimal weight vector w
∗
for the problem
min
w∈R
n
kV
π
−V
w
k
ξ,2
, V
w
(x) = φ(x)
>
w . (9.8)
Of note, the optimal approximation V
w
∗
is also the solution to the problem
min
w∈R
n
E[kG
π
−V
w
k
ξ,2
] . (9.9)
Consequently, a simple approach for finding
w
∗
is to perform stochastic gradient
descent with a loss function that reflects Equation 9.9. For
x ∈X
and
z ∈R
, let
us define the sample loss
L(w) =
z −φ(x)
>
w
2
whose gradient with respect to w is
∇
w
L(w) = −2
z −φ(x)
>
w
φ(x) .
Stochastic gradient descent updates the weight vector
w
by following the (nega-
tive) gradient of the sample loss constructed from each sample. Instantiating
the sample loss with x = x
k
and z = g
k
, this results in the update rule
w ←w + α
k
(g
k
−φ(x
k
)
>
w
φ(x
k
) , (9.10)
where
α
k
∈
[0
,
1) is a time-varying step size that also subsumes the constant
from the loss. Under appropriate conditions, this update rule finds the optimal
weight vector
w
∗
(see, e.g., Bottou 1998). Exercise 9.9 asks you to verify that
the optimal weight vector w
∗
is a fixed point of the expected update.
Let us now consider the problem of learning the value function from a
sequence of sample transitions (
x
k
, a
k
, r
k
, x
0
k
)
k≥0
, again assumed to be indepen-
dent realizations from the appropriate distributions. Given a weight vector
w
,
the temporal-difference learning target for linear value function approximation
is
r
k
+ γV
w
(x
0
k
) = r
k
+ γφ(x
0
k
)
>
w .
We use this target in lieu of
g
k
in Equation 9.10 to obtain the semi-gradient
temporal-difference learning update rule
w ←w + α
k
r
k
+ γφ(x
0
k
)
>
w −φ(x
k
)
>
w
| {z }
TD error
φ(x
k
) , (9.11)
Draft version.
272 Chapter 9
in which the temporal-difference (TD) error appears, now with value function
estimates constructed from linear approximation. By substituting the Monte
Carlo target
g
k
for the temporal-difference target, the intent is to learn an
approximation to
V
π
by a bootstrapping process, as in the tabular setting. The
term “semi-gradient” reflects the fact that the update rule does not actually
follow the gradient of the sample loss
r
k
+ γφ(x
0
k
)
>
w −φ(x
k
)
>
w
2
,
which contains additional terms related to φ(x
0
) (see bibliographical remarks).
We can understand the relationship between semi-gradient temporal-
difference learning and the projected Bellman operator Π
φ,ξ
T
π
by way of an
update rule defined in terms of a second set of weights
˜w
, the target weights.
This update rule is
w ←w + α
k
(r
k
+ γφ(x
0
k
)
>
˜w −φ(x
k
)
>
w
φ(x
k
) . (9.12)
When
˜w
=
w
, this is Equation 9.11. However, if
˜w
is a separate weight vector,
this is the update rule of stochastic gradient descent on the sample loss
r
k
+ γφ(x
0
k
)
>
˜w −φ(x
k
)
>
w
2
.
Consequently, this update rule finds a weight vector
w
∗
that approximately
minimizes
kT
π
V
˜w
−V
w
k
ξ,2
,
and Equation 9.12 describes an incremental algorithm for computing a single
step of the projected Bellman operator applied to V
˜w
; its solution w
∗
satisfies
Φw
∗
= Π
φ,ξ
T
π
V
˜w
.
This argument suggests that semi-gradient temporal-difference learning tracks
the behavior of the projected Bellman operator. In particular, at the fixed point
ˆ
V
π
= Φ
ˆw
of this operator, semi-gradient TD learning (applied to realizations
from the sample transition model (
X, A, R, X
0
), with
X ∼ξ
) leaves the weight
vector unchanged, in expectation.
E
π
R + γφ(X
0
)
>
ˆw −φ(X)
>
ˆw
φ(X)
= 0 .
In semi-gradient temporal-difference learning, however, the sample target
r
k
+
γφ
(
x
0
k
)
>
w
depends on
w
and is used to update
w
itself. This establishes
a feedback loop that, combined with function approximation, can result in
divergence – even when the projected Bellman operator is well behaved. The
following example illustrates this phenomenon.
Draft version.
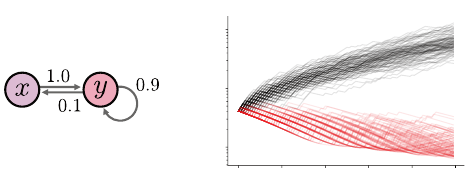
Linear Function Approximation 273
0 20 40 60 80 100
Iteration
10
0
10
1
10
2
Approximation error (log)
(a) (b)
Figure 9.2
(a)
A Markov decision process for which semi-gradient temporal-difference learning can
diverge.
(b)
Approximation error (measured in unweighted
L
2
norm) over the course of
100 runs of the algorithm with
α
= 0
.
01 and the same initial condition
w
0
= (1
,
0
,
0) but
different draws of the sample transitions. Black and red lines indicate runs with
ξ
(
x
) =
1
/2
and
1
/11, respectively.
Example 9.9
(Baird’s counterexample (Baird 1995))
.
Consider the Markov
decision process depicted in Figure 9.2a and the state representation
φ(x) = (1, 3, 2) φ(y) = (4, 3, 3).
Since the reward is zero everywhere, the value function for this MDP is
V
π
= 0.
However, if X
k
∼ξ with ξ(x) = ξ(y) = 1/2, the semi-gradient update
w
k+1
= w
k
+ α(0 + γφ(X
0
k
)
>
w
k
−φ(X
k
)
>
w
k
)φ(X
k
)
diverges unless
w
0
= 0. Figure 9.2b depicts the effect of this divergence on the
approximation error: on average, the distance to the fixed point
k
Φ
w
k
−
0
k
ξ,2
grows exponentially with each update. Also shown is the approximation error
over time if we take ξ to be the steady-state distribution
ξ(x) =
1
/11 ξ(y) =
10
/11,
in which case the approximation error becomes close to zero as
k →∞
. This
demonstrates the impact of the relative update frequency of different states on
the behavior of the algorithm.
On the other hand, note that the basis functions implied by
φ
span
R
X
and
thus
Π
φ,ξ
T
π
V = T
π
V
for any
V ∈R
2
. Hence, the iterates
V
k+1
= Π
φ,ξ
T
π
V
k
in this case converge to
0 for any initial
V
0
∈R
2
. This illustrates that requiring the convergence that
the sequence of iterates derived from the projected Bellman operator is not
sufficient to guarantee the convergence of the semi-gradient iterates. 4
Draft version.

274 Chapter 9
Example 9.9 illustrates how reinforcement learning with function approx-
imation is a more delicate task than in the tabular setting. If states are
updated proportionally to their steady-state distribution, however, a convergence
guarantee becomes possible (see bibliographical remarks).
9.5 Semi-Gradient Algorithms for Distributional Reinforcement
Learning
With the right modeling tools, function approximation can also be used to
tractably represent the return functions of large problems. One difference with
the expected-value setting is that it is typically more challenging to construct
an approximation that is linear in the true sense of the word. With linear
value function approximations, adding weight vectors is equivalent to adding
approximations:
V
w
1
+w
2
(x) = V
w
1
(x) + V
w
2
(x) .
In the distributional setting, the same cannot apply because probability dis-
tributions do not form a vector space. This means that we cannot expect a
return-distribution function representation to satisfy
η
w
1
+w
2
(x)
?
= η
w
1
(x) + η
w
2
(x) ; (9.13)
the right-hand side is not a probability distribution (it is, however, a signed
distribution: more on this in Section 9.6). An alternative is to take a slightly
broader view and consider distributions whose parameters depend linearly on
w
. There are now two sources of approximation: one due to the finite parameter-
ization of probability distributions in
F
, another because those parameters are
themselves aliased. This is an expressive framework, albeit one under which
the analysis of algorithms is significantly more complex.
Linear QTD.
Let us first derive a linear approximation of quantile temporal-
difference learning. Linear QTD represents the locations of quantile distri-
butions using linear combinations of features. If we write
w ∈R
m×n
for the
matrix whose columns are
w
1
, . . . , w
m
∈R
n
, then the linear QTD return function
estimate takes the form
η
w
(x) =
1
m
m
X
i=1
δ
φ(x)
>
w
i
.
One can verify that
η
w
(
x
) is not a linear combination of features, even though
its parameters are. We construct the linear QTD update rule by following the
negative gradient of the quantile loss (Equation 6.12), taken with respect to the
parameters w
1
, . . . , w
m
. We first rewrite this loss in terms of a function ρ
τ
:
ρ
τ
(∆) = |
{∆ < 0}
−τ|×|∆|
Draft version.

Linear Function Approximation 275
so that for a sample
z ∈R
and estimate
θ ∈R
, the loss of Equation 6.12 can be
expressed as
|
{z < θ}
−τ|×|z −θ|= ρ
τ
(z −θ) .
We instantiate the quantile loss with
θ
=
φ
(
x
)
>
w
i
and
τ
=
τ
i
=
2i−1
2m
to obtain the
loss
L
τ
i
(w) = ρ
τ
i
(z −φ(x)
>
w
i
) . (9.14)
By the chain rule, the gradient of this loss with respect to w
i
is
∇
w
i
ρ
τ
i
(z −φ(x)
>
w
i
) = −(τ
i
− {z < φ(x)
>
w
i
})φ(x) . (9.15)
As in our derivation of QTD, from a sample transition (
x, a, r, x
0
), we construct
m sample targets:
g
j
= r + γφ(x
0
)
>
w
j
, j = 1, . . . , m .
By instantiating the gradient expression in Equation 9.15 with
z
=
g
j
and taking
the average over the m sample targets, we obtain the update rule
w
i
←w
i
−α
1
m
m
X
j=1
∇
w
i
ρ
τ
i
g
j
−φ(x)
>
w
i
,
which is more explicitly
w
i
←w
i
+ α
1
m
m
X
j=1
τ
i
− {g
j
< φ(x)
>
w
i
}
| {z }
quantile TD error
φ(x). (9.16)
Note that, by plugging
g
j
into the expression for the gradient (Equation 9.15),
we obtain a semi-gradient update rule. That is, analogous to the value-based
case, Equation 9.16 is not equivalent to the gradient update
w
i
←w
i
−α
1
m
m
X
j=1
∇
w
i
ρ
τ
i
r + γφ(x
0
)
>
w
j
−φ(x)
>
w
i
,
because in general
∇
w
i
ρ
τ
i
r + γφ(x
0
)
>
w
i
−φ(x)
>
w
i
,
τ
i
− {g
i
< φ(x)
>
w
i
}
φ(x) .
Linear CTD.
To derive a linear approximation of categorical temporal-
difference learning, we represent the probabilities of categorical distributions
using linear combinations of features. Specifically, we apply the softmax func-
tion to transform the parameters (
φ
(
x
)
>
w
i
)
m
i=1
into a probability distribution. We
write
p
i
(x; w) =
e
φ(x)
>
w
i
m
P
j=1
e
φ(x)
>
w
j
. (9.17)
Draft version.
276 Chapter 9
Recall that the probabilities
p
i
(
x
;
w
))
m
i=1
correspond to
m
locations (
θ
i
)
m
i=1
. The
softmax transformation guarantees that the expression
η
w
(x) =
m
X
i=1
p
i
(x; w)δ
θ
i
describes a bona fide probability distribution. We thus construct the sample
target ¯η(x):
¯η(x) = Π
c
(b
r,γ
)
#
η
w
(x
0
) = Π
c
h
m
X
i=1
p
i
(x
0
; w)δ
r+γθ
i
i
=
m
X
i=1
¯p
i
δ
θ
i
,
where
¯p
i
denotes the probability assigned to the location
θ
i
by the sample target
¯η
(
x
). Expressed in terms of the CTD coefficients (Equation 6.10), the probability
¯p
i
is
¯p
i
=
m
X
j=1
ζ
i, j
(r)p
j
(x
0
; w) .
As with quantile regression, we adjust the weights
w
by means of a gradient
descent procedure. Here, we use the cross-entropy loss between
η
w
(
x
) and
¯η(x):
72
L(w) = −
m
X
i=1
¯p
i
log p
i
(x; w). (9.18)
Combined with the softmax function, Equation 9.18 becomes
L(w) = −
m
X
i=1
¯p
i
φ(x)
>
w
i
−log
m
X
j=1
e
φ(x)
>
w
j
.
With some algebra and again invoking the chain rule, we obtain that the gradient
with respect to the weights w
i
is
∇
w
i
L(w) = −
¯p
i
− p
i
(x; w)
φ(x) .
By adjusting the weights in the opposite direction of this gradient, this results
in the update rule
w
i
←w
i
+ α
¯p
i
− p
i
(x; w)
| {z }
CTD error
φ(x). (9.19)
72.
The choice of cross-entropy loss is justified because it is the matching loss for the softmax
function, and their combination results in a convex objective (Auer et al. 1995; see also Bishop
2006, Section 4.3.6).
Draft version.
Linear Function Approximation 277
While interesting in their own right, linear CTD and QTD are particularly
important in that they can be straightforwardly adapted to learn return-
distribution functions with nonlinear function approximation schemes such
as deep neural networks; we return to this point in Chapter 10. For now, it is
worth noting that the update rules of linear TD, linear QTD, and linear CTD
can all be expressed as
w
i
←w
i
+ αε
i
φ(x) ,
where
ε
i
is an error term. One interesting difference is that for both linear
CTD and linear QTD,
ε
i
lies in the interval [
−
1
,
1], while for linear TD, it
is unbounded. This gives evidence that we should expect different learning
dynamics from these algorithms. In addition, combining linear TD or linear
QTD to a tabular state representation recovers the corresponding incremen-
tal algorithms from Chapter 6. For linear CTD, the update corresponds to a
tabular representation of the softmax parameters rather than the probabilities
themselves, and the correspondence is not as straightforward.
Analyzing linear QTD and CTD is complicated by the fact that the return
functions themselves are not linear in
w
1
, . . . , w
m
. One solution is to relax the
requirement that the approximation
η
w
(
x
) be a probability distribution; as we
will see in the next section, in this case the distributional approximation behaves
much like the value function approximation, and a theoretical guarantee can be
obtained.
9.6 An Algorithm Based on Signed Distributions*
So far, we made sure that the outputs of our distributional algorithms were valid
probability distributions (or could be as interpreted as such: for example, when
working with statistical functionals). This was done explicitly when using the
softmax parameterization in defining linear CTD and implicitly in the mixture
update rule of CTD in Chapter 3. In this section, we consider an algorithm that
is similar to linear CTD but omits the softmax function. As a consequence of
this change, this modified algorithm’s outputs are signed distributions, which
we briefly encountered in Chapter 6 in the course of analyzing categorical
temporal-difference learning.
Compared to linear CTD, this approach has the advantage of being both
closer to the tabular algorithm (it finds a best fit in
2
distance, like tabular
CTD) and closer to linear value function approximation (making it amenable
to analysis). Although the learned predictions lack some aspects of probability
distributions – such as well-defined quantiles – the learned signed distributions
can be used to estimate expectations of functions, including expected values.
Draft version.
278 Chapter 9
To begin, let us define a (finite) signed distribution
ν
as a weighted sum of
two probability distributions:
ν = λ
1
ν
1
+ λ
2
ν
2
λ
1
, λ
2
∈R , ν
1
, ν
2
∈P(R) . (9.20)
We write
M
(
R
) for the space of finite signed distributions. For
ν ∈M
(
R
)
decomposed as in Equation 9.20, we define its cumulative distribution function
F
ν
and the expectation of a function f : R →R as
F
ν
(z) = λ
1
F
ν
1
(z) + λ
2
F
ν
2
(z), z ∈R
E
Z∼ν
[ f (Z)] = λ
1
E
Z∼ν
1
[ f (Z)] + λ
2
E
Z∼ν
2
[ f (Z)] . (9.21)
Exercise 9.14 asks you to verify that these definitions are independent of the
decomposition of
ν
into a sum of probability distributions. The total mass of
ν
is given by
κ(ν) = λ
1
+ λ
2
.
We make these definitions explicit because signed distributions are not proba-
bility distributions; in particular, we cannot draw samples from
ν
. In that sense,
the notation
Z ∼ν
in the definition of expectation is technically incorrect, but
we use it here for convenience.
Definition 9.10.
The signed
m
-categorical representation parameterizes the
mass of m particles at fixed locations (θ
i
)
m
i=1
:
F
S,m
=
n
m
X
i=1
p
i
δ
θ
i
: p
i
∈R for i = 1, . . . , m,
m
X
i=1
p
i
= 1
o
. 4
Compared to the usual
m
-categorical representation, its signed analogue
adds a degree of freedom: it allows the mass of its particles to be negative and
of magnitude greater than 1 (we reserve “probability” for values strictly in
[0
,
1]). However, in our definition, we still require that signed
m
-categorical
distributions have unit total mass; as we will see, this avoids a number of
technical difficulties. Exercise 9.15 asks you to verify that ν ∈F
S,m
is a signed
distribution in the sense of Equation 9.20.
Recall from Section 5.6 that the categorical projection Π
c
:
P
(
R
)
→F
C,m
is
defined in terms of the triangular and half-triangular kernels
h
i
:
R →
[0
,
1],
i
=
1
, . . . , m
. We use Equation 9.21 to extend this projection to signed distributions,
written Π
c
:
M
(
R
)
→F
S,m
. Given
ν ∈M
(
R
), the masses of Π
c
ν
=
P
m
i=1
p
i
δ
θ
i
are
given by
p
i
= E
Z∼ν
h
i
ς
−1
m
(Z −θ
i
)
,
where as before,
ς
−1
m
=
θ
i+1
−θ
i
(
i < m
), and we write
E
Z∼ν
in the sense of Equation
9.21. We also extend the notation to signed return-distribution functions in the
Draft version.

Linear Function Approximation 279
usual way. Observe that if
ν
is a probability distribution, then Π
c
ν
matches our
earlier definition. The distributional Bellman operator, too, can be extended
to signed distributions. Let
η ∈M
(
R
)
X
be a signed return function. We define
T
π
: M (R)
X
→M (R)
X
:
(T
π
η)(x) = E
π
[(b
R,γ
)
#
η(X
0
) |X = x] .
This is the same equation as before, except that now the operator constructs
convex combinations of signed distributions.
Definition 9.11.
Given a state representation
φ
:
X→R
n
and evenly spaced
particle locations
θ
1
, …, θ
m
, a signed linear return function approximation
η
w
∈F
X
S,m
is parameterized by a weight matrix
w ∈R
n×m
and maps states to
signed return function estimates according to
η
w
(x) =
m
X
i=1
p
i
(x; w)δ
θ
i
, p
i
(x; w) = φ(x)
>
w
i
+
1
m
1 −
m
X
j=1
φ(x)
>
w
j
, (9.22)
where
w
i
is the
i
th column of
w
. We denote the space of signed return functions
that can be represented in this form by F
φ,S,m
. 4
Equation 9.22 can be understood as approximating the mass of each particle
linearly and then adding mass to all particles uniformly to normalize the signed
distribution to have unit total mass. It defines a subset of signed
m
-categorical
distributions that are constructed from linear combinations of features. Because
of the normalization, and unlike the space of linear value function approxima-
tions constructed from
φ
,
F
φ,S,m
is not a linear subspace of
M
(
R
). However,
for each x ∈X, the mapping
w 7→η
w
(x)
is said to be affine, a property that is sufficient to permit theoretical analysis
(see Remark 9.3).
Using a linearly parameterized representation of the form given in Equa-
tion 9.22, we seek to build a distributional dynamic programming algorithm
based on the signed categorical representation. The complication now is that the
distributional Bellman operator takes the return function approximation away
from our linear parameterization in two separate ways: first, the distributions
themselves may move away from the categorical representation, and second, the
distributions may no longer be representable by a linear combination of features.
We address these issues with a doubly projected distributional operator:
Π
φ,ξ,
2
Π
c
T
π
,
where the outer projection finds the best approximation to Π
c
T
π
in F
φ,S,m
. By
analogy with the value-based setting, we define “best approximation” in terms
Draft version.
280 Chapter 9
of a ξ-weighted Cramér distance, denoted
ξ,2
:
2
2
(ν, ν
0
) =
Z
R
(F
ν
(z) −F
ν
0
(z))
2
dz ,
2
ξ,2
(η, η
0
) =
X
x∈X
ξ(x)
2
2
η(x), η
0
(x)
,
Π
φ,ξ,
2
η = arg min
η
0
∈F
φ,S,m
2
ξ,2
(η, η
0
) .
Because we are now dealing with signed distributions, the Cramér distance
2
2
(
ν, ν
0
) is infinite if the two input signed distributions
ν, ν
0
do not have the same
total mass. This justifies our restriction to signed distributions with unit total
mass in defining both the signed
m
-categorical representation and the linear
approximation. The following lemma shows that the distributional Bellman
operator preserves this property (see Exercise 9.16).
Lemma 9.12.
Suppose that
η ∈M
(
R
)
X
is a signed return-distribution function.
Then,
κ
(T
π
η)(x)
=
X
x
0
∈X
P
π
(X
0
= x
0
| X = x)κ
η(x
0
)
.
In particular, if all distributions of
η
have unit total mass – that is,
κ
(
η
(
x
)) = 1
for all x – then
κ
(T
π
η)(x)
= 1 . 4
While it is possible to derive algorithms that are not restricted to outputting
signed distributions with unit total mass, one must then deal with added com-
plexity due to the distributional Bellman operator moving total mass from state
to state.
We next derive a semi-gradient update rule based on the doubly projected
Bellman operator. Following the unbiased estimation method for designing
incremental algorithms (Section 6.2), we construct the signed target
Π
c
˜η(x) = Π
c
(b
r,γ
)
#
η
w
(x
0
) .
Compared to the sample target of Equation 6.9, here
η
w
is a signed return
function in F
X
S,m
.
The semi-gradient update rule adjusts the weight vectors
w
i
to minimize the
2
distance between Π
c
˜η
(
x
) and the predicted distribution
η
w
(
x
). It does so by
taking a step in direction of the negative gradient of the squared
2
distance
73
w
i
←w
i
−α∇
w
i
2
2
(η
w
(x), Π
c
˜η(x)) .
73. In this expression, ˜η(x) is used as a target estimate and treated as constant with regards to w.
Draft version.

Linear Function Approximation 281
We obtain an implementable version of this update rule by expressing distri-
butions in
F
S,m
in terms of
m
-dimensional vectors of masses. For a signed
categorical distribution
ν =
m
X
i=1
p
i
δ
θ
i
,
let us denote by
p ∈R
m
the vector (
p
1
, …, p
m
); similarly, denote by
p
0
the
vector of masses for a signed distribution
ν
0
. Because the cumulative functions
of signed categorical distributions with unit total mass are constant on the
intervals [θ
i
, θ
i+1
] and equal outside of the [θ
1
, θ
m
] interval, we can write
2
2
(ν, ν
0
) =
Z
R
F
ν
(z) −F
ν
0
(z)
2
dz
= ς
m
m−1
X
i=1
F
ν
(θ
i
) −F
ν
0
(θ
i
)
2
= ς
m
kCp −C p
0
k
2
2
, (9.23)
where
k·k
2
is the usual Euclidean norm and
C ∈R
m×m
is the lower-triangular
matrix
C =
1 0 ··· 0 0
1 1 ··· 0 0
.
.
.
.
.
.
.
.
.
1 1 ··· 1 0
1 1 ··· 1 1
.
Letting
p
(
x
) and
˜p
(
x
) denote the vector of masses for the signed approximation
η
w
(
x
) and the signed target Π
c
˜η
(
x
), respectively, we rewrite the above in terms
of matrix-vector operations (Exercise 9.17 asks you to derive the gradient of
2
2
with respect to w
i
):
w
i
←w
i
+ ας
m
( ˜p(x) − p(x))
>
C
>
C ˜e
i
φ(x) , (9.24)
where ˜e
i
∈R
m
is a vector whose entries are
˜e
i j
=
{i = j}
−
1
m
.
By precomputing the vectors
C
>
C ˜e
i
, this update rule can be applied in
O
(
m
2
+
mn) operations per sample transition.
9.7 Convergence of the Signed Algorithm*
We now turn our attention to establishing a contraction result for the doubly
projected Bellman operator, by analogy with Theorem 9.8. We write
M
2
,1
(R) = {λ
1
ν
1
+ λ
2
ν
2
: λ
1
, λ
2
∈R, λ
1
+ λ
2
= 1, ν
1
, ν
2
∈P
2
(R)},
Draft version.

282 Chapter 9
for finite signed distributions with unit total mass and finite Cramér distance
from one another. In particular, note that F
S,m
⊆M
2
,1
(R).
Theorem 9.13.
Suppose Assumption 4.29(1) holds and that Assump-
tion 9.5 holds with unique stationary distribution
ξ
π
. Then the pro-
jected operator Π
φ,ξ
π
,
2
Π
c
T
π
:
M
2
,1
(
R
)
X
→M
2
,1
(
R
)
X
is a contraction with
respect to the metric
ξ
π
,2
, with contraction modulus γ
1
/2
. 4
This result is established by analyzing separately each of the three operators
that composed together constitute the doubly projected operator Π
φ,ξ
π
,
2
Π
c
T
π
.
Lemma 9.14.
Under the assumptions of Theorem 9.13,
T
π
:
M
2
,1
(
R
)
→
M
2
,1
(R) is a γ
1
/2
-contraction with respect to
ξ
π
,2
. 4
Lemma 9.15.
The categorical projection operator Π
c
:
M
2
,1
(
R
)
→F
S,m
is a
nonexpansion with respect to
2
. 4
Lemma 9.16.
Under the assumptions of Theorem 9.13, the function approxima-
tion projection operator Π
φ,ξ
π
,
2
:
F
X
S,m
→F
X
S,m
is a nonexpansion with respect
to
ξ
π
,2
. 4
The proof of Lemma 9.14 essentially combines the reasoning of Proposi-
tion 4.20 and Lemma 9.6 and so is left as Exercise 9.18. Similarly, the proof of
Lemma 9.15 follows according to exactly the same calculations as in the proof
of Lemma 5.23, and so it is left as Exercise 9.19. The central observation is
that the corresponding arguments made for the Cramér distance in Chapter 5
under the assumption of probability distributions do not actually make use of
the monotonicity of the cumulative distribution functions and so extend to the
signed distributions under consideration here.
Proof of Lemma 9.16.
Let
η, η
0
∈F
X
S,m
and write
p
(
x
),
p
0
(
x
) for the vector of
masses of η(x) and η
0
(x), respectively. From Equation 9.23, we have
2
ξ
π
,2
(η, η
0
) =
X
x∈X
ξ
π
(x)
2
2
(η(x), η
0
(x))
=
X
x∈X
ξ
π
(x)ς
m
kCp(x) −C p
0
(x)k
2
2
= ς
m
kp − p
0
k
2
Ξ⊗C
>
C
,
where Ξ
⊗C
>
C
is a positive semi-definite matrix in
R
(X×m)×(X×m)
, with Ξ =
diag
(
ξ
π
)
∈R
X×X
, and
p, p
0
∈R
X×m
are the vectorized probabilities associated
with
η, η
0
. Therefore, Π
φ,ξ
π
,
2
can be interpreted as a Euclidean projection under
Draft version.

Linear Function Approximation 283
the norm
k·k
Ξ⊗C
>
C
and hence is a nonexpansion with respect to the corre-
sponding norm; the result follows as this norm precisely induces the metric
ξ
π
,2
.
Proof of Theorem 9.13.
We use similar logic to that of Lemma 5.21 to com-
bine the individual contraction results established above, taking care that the
operators to be composed have several different domains between them. Let
η, η
0
∈M
2
,1
(R)
X
. Then note that
ξ
π
,2
(Π
φ,ξ
π
,
2
Π
c
T
π
η, Π
φ,ξ
π
,
2
Π
c
T
π
η
0
)
(a)
≤
ξ
π
,2
(Π
c
T
π
η, Π
c
T
π
η
0
)
(b)
≤
ξ
π
,2
(T
π
η, T
π
η
0
)
(c)
≤γ
1
/2
ξ
π
,2
(η, η
0
) ,
as required. Here, (a) follows from Lemma 9.16, since Π
c
T
π
η,
Π
c
T
π
η
0
∈
F
X
S,m
. (b) follows from Lemma 9.15 and the straightforward corollary that
ξ
π
,2
(Π
c
η,
Π
c
η
0
)
≤
ξ
π
,2
(
η, η
0
) for
η, η
0
∈M
2
,1
(
R
). Finally, (c) follows from
Lemma 9.14.
The categorical projection is a useful computational device as it allows Π
φ,ξ,
2
to be implemented strictly in terms of signed
m
-categorical representations,
and we rely on it in our analysis. Mathematically, however, it is not strictly
necessary as it is implied by the projection onto the
F
φ,S,m
; this is demonstrated
by the following Pythagorean lemma.
Lemma 9.17.
For any signed
m
-categorical distribution
ν ∈F
S,m
(for which
ν = Π
c
ν) and any signed distribution ν
0
∈M
2
,1
(R),
2
2
(ν, ν
0
) =
2
2
(ν, Π
c
ν
0
) +
2
2
(Π
c
ν
0
, ν
0
) . (9.25)
Consequently, for any η ∈M
2
,1
(R),
Π
φ,ξ,
2
Π
c
T
π
η = Π
φ,ξ,
2
T
π
η . 4
Equation 9.25 is obtained by a similar derivation to the one given in Remark
5.4, which proves the identity when
ν
and
ν
0
are the usual
m
-categorical
distributions.
Just as in the case studied in Chapter 5 without function approximation, it
is now possible to establish a guarantee on the quality of the fixed point of the
operator Π
φ,ξ
π
,
2
Π
C
T
π
.
Draft version.

284 Chapter 9
Proposition 9.18.
Suppose that the conditions of Theorem 9.13 hold, and
let
ˆη
π
s
be the resulting fixed point of the projected operator Π
φ,ξ
π
,
2
Π
C
T
π
.
We have the following guarantee on the quality of
ˆη
π
s
compared with the
(
2,ξ
π
, F
φ,S,m
)-optimal approximation of η
π
: namely, Π
φ,ξ
π
,
2
η
π
:
ξ
π
,2
(η
π
, ˆη
π
s
) ≤
ξ
π
,2
(η
π
, Π
φ,ξ
π
,
2
η
π
)
p
1 −γ
. 4
Proof. We calculate directly:
2
ξ
π
,2
(η
π
, ˆη
π
s
)
(a)
=
2
ξ
π
,2
(η
π
, Π
φ,ξ
π
,
2
Π
c
η
π
) +
2
ξ
π
,2
(Π
φ,ξ
π
,
2
Π
c
η
π
, Π
φ,ξ
π
,
2
Π
c
ˆη
π
s
)
(b)
=
2
ξ
π
,2
(η
π
, Π
φ,ξ
π
,
2
Π
c
η
π
) +
2
ξ
π
,2
(Π
φ,ξ
π
,
2
Π
c
T
π
η
π
, Π
φ,ξ
π
,
2
Π
c
T
π
ˆη
π
s
)
(c)
≤
2
ξ
π
,2
(η
π
, Π
φ,ξ
π
,
2
Π
c
η
π
) + γ
2
ξ
π
,2
(η
π
, ˆη
π
s
)
=⇒
2
ξ
π
,2
(η
π
, ˆη
π
s
) ≤
1
1 −γ
2
ξ
π
,2
(η
π
, Π
φ,ξ
π
,
2
Π
c
η
π
) ,
where (a) follows from the Pythagorean identity in Lemma 9.17 and a similar
identity concerning Π
φ,ξ
π
,
2
, (b) follows since
η
π
is fixed by
T
π
and
ˆη
π
s
is fixed
by Π
φ,ξ
π
,
2
Π
C
T
π
, and (c) follows from
γ
1
/2
-contractivity of Π
φ,ξ
π
,
2
Π
C
T
π
in
2,ξ
π
.
This result provides a quantitative guarantee on how much the approximation
error compounds when
ˆη
π
s
is computed by approximate dynamic programming.
Of note, here there are two sources of error: one due to the use of a finite
number
m
of distributional parameters and another due to the use of function
approximation.
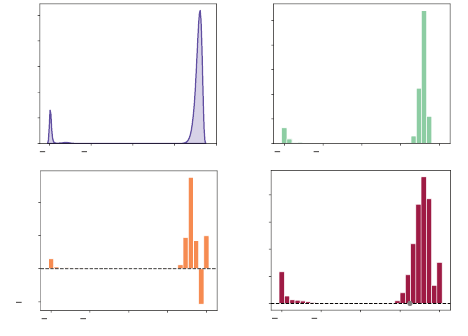
Example 9.19.
Consider linearly approximating the return-distribution func-
tion of the safe policy in the Cliffs domain (Example 2.9). If we use a
three-dimensional state representation
φ
(
x
) = [1
, x
r
, r
c
] where
x
r
, x
c
are the
row and column indices of a given state, then we observe aliasing in the
approximated return distribution (Figure 9.3). In addition, the use of a signed
distribution representation results in negative mass being assigned to some
locations in the optimal approximation. This is by design; given the limited
capacity of the approximation, the algorithms find a solution that mitigates
errors at some locations by introducing negative mass at other locations. As
usual, the use of a bootstrapping procedure introduces diffusion error, here quite
significant due to the low-dimensional state representation. 4
Draft version.
Linear Function Approximation 285
1.0 0.5 0.0 0.5 1.0
Return
0
2
4
6
8
10
Density
1.0 0.5 0.0 0.5 1.0
Return
0.2
0.0
0.2
0.4
Mass
1.0 0.5 0.0 0.5 1.0
Return
0.00
0.05
0.10
0.15
0.20
Mass
1.0 0.5 0.0 0.5 1.0
Return
0.0
0.1
0.2
0.3
0.4
0.5
Probability
(a) (b)
(c) (d)
Figure 9.3
Signed linear approximations of the return distribution of the initial state in Example 2.9.
(a–b)
Ground-truth return-distribution function and categorical Monte Carlo approxima-
tion, for reference. (
c
) Best approximation from
F
φ,S,m
based on the state representation
φ
(
x
) = [1
, x
r
, r
c
] where
x
r
, x
c
are the row and column indices of a given state, with (0
,
0)
denoting the top-left corner. (d) Fixed point of the signed categorical algorithm.
9.8 Technical Remarks
Remark 9.1.
For finite action spaces, we can easily convert a state represen-
tation
φ
(
x
) to a state-action representation
φ
(
x, a
) by repeating a basic feature
matrix Φ
∈R
X×n
. Let
N
A
be the number of actions. We build a block-diagonal
feature matrix Φ
X,A
∈R
(X×A)×(nN
A
)
that contains N
A
copies of Φ:
Φ
X,A
:=
Φ 0 ··· 0
0 Φ ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· Φ
.
The weight vector w is also extended to be of dimension nN
A
, so that
Q
w
(x, a) =
Φ
X,A
w
(x, a)
as before. This is equivalent to but somewhat more verbose than the use of
per-action weight vectors. 4
Remark 9.2.
Assumption 9.5 enabled us to demonstrate that the projected
Bellman operator Π
φ,ξ
T
π
has a unique fixed point, by invoking Banach’s fixed
point theorem. The first part of the assumption, on the uniqueness of
ξ
π
, is
relatively mild and is only used to simplify the exposition. However, if there
Draft version.

286 Chapter 9
is a state
x
for which
ξ
π
(
x
) = 0, then
k·k
ξ
π
,2
does not define a proper metric on
R
n
and Banach’s theorem cannot be used. In this case, there might be multiple
fixed points (see Exercise 9.7).
In addition, if we allow
ξ
π
to assign zero probability to some states, the
norm
k·k
ξ
π
,2
may not be a very interesting measure of accuracy. One common
situation where the issue arises is when there is a terminal state
x
∅
that is
reached with probability 1, in which case
lim
t→∞
P
π
(X
t
= x
∅
) = 1 .
It is easy to see that in this case,
ξ
π
puts all of its probability mass on
x
∅
, so
that Theorem 9.8 becomes vacuous: the norm
k·k
ξ
π
,2
only measures the error at
the terminal state. A more interesting distribution to consider is the distribution
of states resulting from immediately resetting to an initial state when
x
∅
is
reached. In particular, this corresponds to the distribution used in many practical
applications. Let
ξ
0
be the initial state distribution; without loss of generality,
let us assume that ξ
0
(x
∅
) = 0. Define the substochastic transition operator
P
X,∅
(x
0
| x, a) =
(
0 if x
0
= x
∅
,
P
X
(x
0
| x, a) otherwise.
In addition, define a transition operator that replaces transitions to the terminal
state by transition to one of the initial states, according to the initial distribution
ξ
0
:
P
X,ξ
0
(x
0
| x, a) = P
X,∅
(x
0
| x, a) +
{x
0
, x
∅
}
P
X
(x
∅
| x, a)ξ
0
(x
0
) .
One can show that the Bellman operator T
π
∅
(defined from P
X,∅
) satisfies
T
π
∅
V = T
π
V
for any
V ∈R
X
for which
V
(
x
∅
) = 0 and that the steady-state distribution
ξ
∅
induced by P
X,ξ
0
and a policy π is such that
there exists t ∈N, P
π
(X
t
= x) > 0 =⇒ ξ
∅
(x) > 0 .
Let P
π
∅
be the transition matrix corresponding to P
X,∅
(x
0
| x, a) and the policy
π. Exercise 9.21 asks you to prove that
kP
π
∅
k
ξ
∅
,2
≤1 ,
from which a modified version of Theorem 9.8 can be obtained. 4
Remark 9.3.
Let
M
and
M
0
be vector spaces. A mapping
O
:
M → M
0
is said
to be affine if, for any U, U
0
∈ M and α ∈[0, 1],
O(αU + (1 −α)U
0
) = αOU + (1 −α)OU
0
.
Draft version.

Linear Function Approximation 287
When
η
w
is a signed linear return function approximation parameterized by
w
,
the map
w 7→η
w
(x)
is affine for each
x ∈X
, as we now show. It is this property that allows us to
express the
2
distance between
ν, ν
0
∈F
S,m
in terms of a difference of vectors
of probabilities (Equation 9.23), needed in the proof of Lemma 9.16.
Let
w, w
0
∈R
n×m
be the parameters of signed return functions of the form of
Equation 9.22. For these, write
p
w
(
x
) for the vector of masses determined by
w
:
p
w
(x) = w
>
φ(x) +
1
m
e
1 −e
>
w
>
φ(x)
,
where e is the m-dimensional vector of ones. We then have
m
X
i=1
φ(x)
>
w
i
= e
>
w
>
φ(x) ,
and similarly for w
0
. Hence,
p
αw+(1−α)w
0
(x) = (αw + (1 −α)w
0
)
>
φ(x) −
1
m
ee
>
(αw + (1 −α)w
0
)
>
φ(x)
= αp
w
(x) + (1 −α)p
w
0
(x) .
We conclude that w 7→η
w
(x) is indeed affine in w. 4
9.9 Bibliographical Remarks
9.1–9.2.
Linear value function approximation as described in this book is in
effect a special case of linear regression where the inputs are taken from a
finite set (
φ
(
x
))
x∈X
and noiseless labels; see Strang (1993), Bishop (2006),
and Murphy (2012) for a discussion on linear regression. Early in the history
of reinforcement learning research, function approximation was provided by
connectionist systems (Barto et al. 1983; Barto et al. 1995) and used to deal
with infinite state spaces (Boyan and Moore 1995; Sutton 1996). An earlier-still
form of linear function approximation and temporal-difference learning was
used by Samuel (1959) to train a strong player for the game of checkers.
9.3.
Bertsekas and Tsitsiklis (1996, Chapter 6) studies linear value function
approximation and its combination with various reinforcement learning meth-
ods, including TD learning (see also Bertsekas 2011, 2012). Tsitsiklis and Van
Roy (1997) establish the contractive nature of the projected Bellman operator
Π
φ,ξ
T
π
under the steady-state distribution (Theorem 9.8 in this book). The
temporal-difference fixed point can be determined directly by solving a least-
squares problem, yielding the least-squares TD algorithm (LSTD; Bradtke and
Barto 1996), which is extended to the control setting by least-squares policy
Draft version.
288 Chapter 9
iteration (LSPI; Lagoudakis and Parr 2003). In the control setting, the method is
also called fitted Q-iteration (Gordon 1995; Ernst et al. 2005; Riedmiller 2005).
Bertsekas (1995) gives an early demonstration that the TD fixed point is in
general different from (and has greater error than) the best approximation to
V
π
, measured in
ξ
-weighted
L
2
norm. However, it is possible to interpret the
temporal-difference fixed point as the solution to an oblique projection problem
that minimizes errors between consecutive states (Harmon and Baird 1996;
Scherrer 2010).
9.4.
Barnard (1993) provides a proof that temporal-difference learning is not
a true gradient-descent method, justifying the term semi-gradient (Sutton and
Barto 2018). The situation in which
ξ
differs from the steady-state (or sampling)
distribution of the induced Markov chain is called off-policy learning; Example
9.9 is a simplified version of the original counterexample due to Baird (1995).
Baird argued for the direct minimization of the Bellman residual by gradient
descent as a replacement to temporal-difference learning, but this method suffers
from other issues and can produce undesirable solutions even in mild scenarios
(Sutton et al. 2008a). The GTD line of work (Sutton et al. 2009; Maei 2011)
is a direct attempt at handling the issue by using a pair of approximations (see
Qu et al. 2019 for applications of this idea in a distributional context); more
recent work directly considers a corrected version of the Bellman residual (Dai
et al. 2018; Chen and Jiang 2019). The convergence of temporal-difference
learning with linear function approximation was proven under fairly general
conditions by Tsitsiklis and Van Roy (1997), using the ODE method from
stochastic approximation theory (Benveniste et al. 2012; Kushner and Yin 2003;
Ljung 1977).
Parr et al. (2007), Parr et al. (2008) and Sutton et al. (2008b) provide a domain-
dependent analysis of linear value function approximation, which is extended
by Ghosh and Bellemare (2020) to establish the existence of representations
that are stable under a greater array of conditions (Exercises 9.10 and 9.11).
Kolter (2011) studies the space of temporal-difference fixed point as a function
of the distribution ξ.
9.5.
Linear CTD and QTD were implicitly introduced by Bellemare et
al. (2017a) and Dabney et al. (2018b), respectively, in the design of deep
reinforcement learning agents (see Chapter 10). Their presentation as given
here is new.
9.6–9.7.
The algorithm based on signed distributions is new to this book. It
improves on an algorithm proposed by Bellemare et al. (2019b) in that it adjusts
the total mass of return distributions to always be 1. Lyle et al. (2019) give
evidence that the original algorithm generally underperforms the categorical
Draft version.
Linear Function Approximation 289
algorithm. They further establish that, in the risk-neutral control setting, distri-
butional algorithms cannot do better than value-based algorithms when using
linear approximation. The reader interested in the theory of signed measures is
referred to Doob (1994).
9.10 Exercises
Exercise 9.1.
Use the update rules of Equation 9.10 and 9.11 to prove the
results from Example 9.1. 4
Exercise 9.2.
Prove that for a linear value function approximation
V
w
= Φ
w
,
we have, for any w, w
0
∈R
n
and α, β ∈R,
V
αw+βw
0
= αV
w
+ βV
w
0
, ∇
w
V
w
(x) = φ(x). 4
Exercise 9.3. In the statement of Proposition 9.3, we required that
(i) the columns of the feature matrix Φ be linearly independent;
(ii) ξ(x) > 0 for all x ∈X.
Explain how the result is affected when either of these requirements is omitted.
4
Exercise 9.4.
Prove Lemma 9.7. Hint. Apply Pythagoras’s theorem to a well-
chosen inner product. 4
Exercise 9.5.
The purpose of this exercise is to empirically study the con-
tractive and expansive properties of the projection in
L
2
norm. Consider an
integer-valued state space
x ∈X
=
{
1
, . . . ,
10
}
with two-dimensional state rep-
resentation
φ
(
x
) = (1
, x
), and write Π
φ
for the
L
2
projection of a vector
v ∈R
X
onto the linear subspace defined by φ. That is,
Π
φ
v = Φ(Φ
>
Φ)
−1
Φ
>
v,
where Φ is the feature matrix.
With this representation, we can represent the vector
u
(
x
) = 0 exactly, and
hence Π
φ
u = u. Now consider the vector u
0
defined by
u
0
(x) = log x.
With a numerical experiment, show that
kΠ
φ
u
0
−Π
φ
uk
2
≤ku
0
−uk
2
but kΠ
φ
u
0
−Π
φ
uk
∞
> ku
0
−uk
∞
. 4
Exercise 9.6.
Provide an example Markov decision process and state represen-
tation that result in the left- and right-hand sides of Equation 9.6 being equal.
Hint. A diagram might prove useful. 4
Draft version.
290 Chapter 9
Exercise 9.7.
Following Remark 9.2, suppose that the steady-state distribution
ξ
π
is such that
ξ
π
(
x
) = 0 for some state
x
. Discuss the implications on the analysis
performed in this chapter, in particular on the set of solutions to Equation 9.8
and the behavior of semi-gradient temporal-difference learning when source
states are drawn from this distribution. 4
Exercise 9.8.
Let
ξ
0
be some initial distribution and
π
a policy. Define the
discounted state-visitation distribution
¯
ξ(x
0
) = (1 −γ)ξ
0
(x
0
) + γ
X
x∈X
P
π
(X
0
= x
0
| X = x)
¯
ξ(x), for all x
0
∈X.
Following the line of reasoning leading to Lemma 9.6, show that the projected
Bellman operator Π
φ,ξ
T
π
is a γ
1
/2
contraction in the
¯
ξ-weighted L
2
metric:
kT
π
k
¯
ξ,2
≤γ
1
/2
. 4
Exercise 9.9.
Let
ξ ∈P
(
X
). Suppose that the feature matrix Φ
∈R
X×n
has
linearly independent columns and
ξ
(
x
)
>
0 for all
x ∈X
. Show that the unique
optimal weight vector w
∗
that is a solution to Equation 9.2 satisfies
E
h
G
π
(X) −φ(X)
>
w
∗
φ(X)
i
= 0, X ∼ξ. 4
Exercise 9.10
(*)
.
This exercise studies the divergence of semi-gradient
temporal-difference learning from a dynamical systems perspective. Recall
that Ξ ∈R
X×X
is the diagonal matrix whose entries are ξ(x).
(i)
Show that in expectation and in matrix form, Equation 9.11 produces the
sequence of weight vectors (w
k
)
k≥0
given by
w
k+1
= w
k
+ α
k
Φ
>
Ξ
r
π
+ γP
π
Φw
k
−Φw
k
).
(ii) Assume that α
k
= α > 0. Express the above as an update of the form
w
k+1
= Aw
k
+ b, (9.26)
where A ∈R
n×n
and b ∈R
n
.
(iii)
Suppose that the matrix
C
= Φ
>
Ξ(
γP
π
−I
)Φ has eigenvalues that are all
real. Show that if one of these is positive, then
A
has at least one eigenvalue
greater than 1.
(iv)
Use the preceding result to conclude that under those conditions, there
exists a w
0
such that kw
k
k
2
→∞.
(v)
Suppose now that all of the matrix
C
’s eigenvalues are real and nonpositive.
Show that in this case, there exists an α ∈(0, 1) such that taking α
k
= α, the
sequence (Φw
k
)
k≥0
converges to the temporal-difference fixed point. 4
Exercise 9.11 (*). Suppose that the state representation is such that
(i) the matrix P
π
Φ ∈R
X×n
has columns that lie in the column span of Φ, and
Draft version.
Linear Function Approximation 291
(ii)
the matrix has columns that are orthogonal with regards to the
ξ
-weighted
inner product. That is,
Φ
>
ΞΦ = I.
Show that in this case, the eigenvalues of the matrix
Φ
>
Ξ(γP
π
−I)Φ
are all nonpositive, for any choice of
ξ ∈P
(
X
). Based on the previous exercise,
conclude on the dynamical properties of semi-gradient temporal-difference
learning with this representation. 4
Exercise 9.12.
Using your favorite numerical computation software, implement
the Markov decision process from Baird’s counterexample (Example 9.9) and
the semi-gradient update
w
k+1
= w
k
+ α
γφ(x
0
k
)w
k
−φ(x
k
)w
k
φ(x
k
) ,
for the state representation of the example and a small, constant value of
α
.
Here, it is assumed that
X
k
has distribution
ξ
and
X
0
k
is drawn from the transition
kernel depicted in Figure 9.2.
(i)
Vary
ξ
(
x
) from 0 to 1, and plot the norm of the value function estimate,
kV
k
k
ξ,2
, as a function of k.
(ii)
Now replace
φ
(
X
0
k
)
w
k
by
φ
(
X
0
k
)
˜w
k
, where
˜w
k
=
w
k−k mod L
for some integer
L ≥
1. That is,
˜w
k
is kept fixed for
L
iterations. Plot the evolution of
kV
k
k
ξ,2
for different values of L. What do you observe? 4
Exercise 9.13.
Repeat Exercise 3.3, replacing the uniform grid encoding the
state with a representation φ defined by
φ(x) =
1, sin(x
1
), cos(x
1
), …, sin(x
4
), cos(x
4
)
,
where (
x
1
, x
2
) denote the Cart–Pole state variables. Implement linear CTD and
QTD and use these with the state representation
φ
to learn a return-distribution
function approximation for the uniform and forward-leaning policies. Visualize
the learned approximations at selected states, including the initial state, and com-
pare them to ground-truth return distributions estimated by the nonparametric
Monte Carlo algorithm (Remark 3.1). 4
Exercise 9.14.
Recall that given a finite signed distribution
ν
expressed as a
sum of probability distributions
ν
=
λ
1
ν
1
+
λ
2
ν
2
(with
λ
1
, λ
2
∈R
,
ν
1
, ν
2
∈P
(
R
)),
we defined expectations under
ν
in terms of sums of expectations under
ν
1
and
ν
2
. Verify that this definition is not dependent on the choice of decomposi-
tion of
ν
into a sum of probability distributions. That is, suppose that there
also exist
λ
0
1
, λ
0
2
∈R
and
ν
0
1
, ν
0
2
∈P
(
R
) with
ν
=
λ
0
1
ν
0
1
+
λ
0
2
ν
0
2
. Show that for any
Draft version.
292 Chapter 9
(measurable) function f : R →R with
E
Z∼ν
1
[|f (Z)|] < ∞, E
Z∼ν
2
[|f (Z)|] < ∞, E
Z∼ν
0
1
[|f (Z)|] < ∞, E
Z∼ν
0
2
[|f (Z)|] < ∞,
we have
λ
1
E
Z∼ν
1
[ f (Z)] + λ
2
E
X∼ν
2
[ f (Z)] = λ
1
E
Z∼ν
0
1
[ f (Z)] + λ
2
E
Z∼ν
0
2
[ f (Z)] . 4
Exercise 9.15.
Show that any
m
-categorical signed distribution
ν ∈F
S,m
can
be written as the weighted sum of two
m
-categorical (probability) distributions
ν
1
, ν
2
∈F
C,m
. 4
Exercise 9.16.
Suppose that we consider a return function
η ∈M
(
R
)
X
defined
over signed distributions (not necessarily with unit total mass). Show that
κ
(T
π
η)(x)
=
X
x
0
∈X
P
π
(X
0
= x | X = x)κ(η(x
0
)) .
Conclude that if η ∈F
X
S,m
, then
κ
(T
π
η)(x)
= 1 . 4
Exercise 9.17.
Consider two signed
m
-categorical distributions
ν, ν
0
∈F
S,m
.
Denote their respective vectors of masses by
p, p
0
∈R
m
. Prove the correctness
of Equation 9.24. That is, show that
∇
w
i
2
2
(ν, ν
0
) = −2ς
m
(p
0
− p)
>
C
>
C ˜e
i
φ(x) . 4
Exercise 9.18. Prove Lemma 9.14. 4
Exercise 9.19. Prove Lemma 9.15. 4
Exercise 9.20. Prove Lemma 9.17. 4
Exercise 9.21. Following the discussion in Remark 9.2, show that
kP
π
∅
k
ξ
∅
,2
≤1 . 4
Draft version.